Enriched profunctors

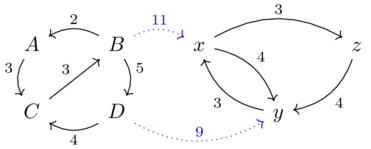
Feasibility relationships as Bool-profunctors(6)
Feasilibiliy relation(1)

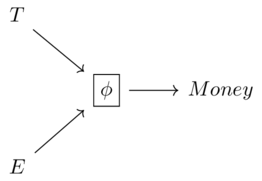
A feasibility relation for preorder \(X\) given preorder \(Y\)

  • A monotone map \(X^{op}\times Y \xrightarrow{\phi} \mathbf{Bool}\)

  • Also denoted \(X \overset{\phi}\nrightarrow Y\)

  • Given \(x \in X, y \in Y\), if \(\phi(x,y)=true\) then we say x can be obtained from y

Linked by

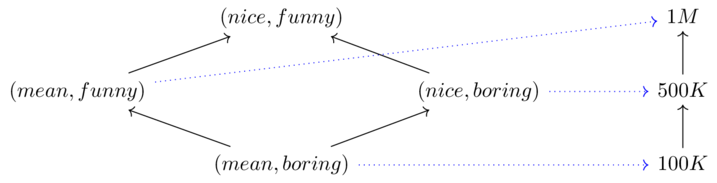
Exercise 4-4(2)

Suppose we have the preorders \(X:=\boxed{monoid\rightarrow category \leftarrow preorder}, Y:=\boxed{nothing \rightarrow thisBook}\)

  1. Draw the Hasse diagram for the preorder \(X^{op} \times Y\)

  2. Write a profunctor \(X \overset{\phi}\nrightarrow Y\)

    • True means “my aunt can explain an x given y"

    • Interpret the fact that the preimage of true is an upper set in \(X^{op}\times Y\)

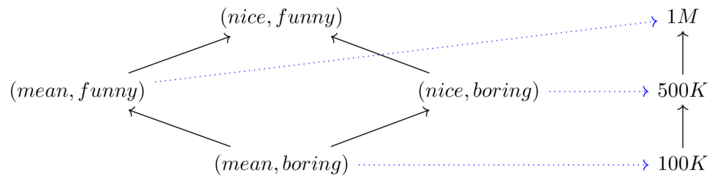
Solution(1)

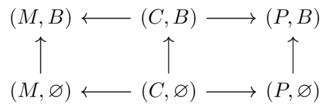
  2. Let \(\phi((M,B))=\phi((P,B))=True\) else \(False\)

    • The preimage of true being an upper set is a consequence of monotone maps to Bool. The domain orders combinations by feasibility (\(x\leq y\) means x is easier than y), and the preimage being an upper set says that if my aunt can explain \(x\) given \(y\), then she can do something easier than \(x\) given \(y\) and can explain \(x\) with something with more explanatory power than \(y\).

Exercise 4-7(2)

Show that the Boolean \(\Rightarrow\) satsifies the requirements of a closure operator.

Solution(1)

This boils down to the tautology that \((a \land v) \implies w\) iff \(a \implies (v \implies w)\), where the last \(\implies\) comes from \(\multimap\) and the others come from \(\leq\).

V-profunctors(12)
V-profunctor(1)
Bool-profunctors(1)

Bool-profunctors and their interpretation as bridges

  • Let’s consider Bool-profunctors. Recall a preorder (Bool-category) can be drawn as a Hasse diagram.

  • A Bool-profunctor \(X \overset{\phi}{\nrightarrow} Y\) can look like this:

  • With bridges coming from the profunctor, one can now use both paths to get from points in \(X\) to points in \(Y\).

  • There is a path from N to e, so \(\phi(N,e)=\)\(true\) but \(\phi(W,d)=\)\(false\).

  • We could put a box around both preorders and define a new preorder, called the collage.

Linked by

Cost-profunctors(1)

Cost profunctors and their interpretation as bridges.

  • Cost categories are Lawvere metric spaces and can be represented by weighted graphs

  • This is a depiction of a Cost-profunctor

  • The distance from a point in the left to a point in the right will run through the left, across a bridge, then through through the right.

  • \(\phi(B,x)=\)\(11\),\(\phi(A,z)=\)\(20\),\(\phi(C,y)=\)\(17\)

Linked by

Exercise 4-10(2)

Is it true that a Bool-profunctor is exactly the same as a feasibility relation?

Solution(1)

Monotone maps are Bool-functors between Bool-categories, so the definitions line up

Exercise 4-12(2)

We can express \(\phi\) as a matrix where the (m,n)th entry is the value of \(\phi(m,n) \in \mathbb{B}\). Fill out the feasibility matrix for this example

Solution(1)

  • \(\phi\) a b c d e
    N T F T F T
    E T T T T T
    W T F T F T
    S T T T T T

Linked by

Exercise 4-15(2)

Fill out the Cost-matrix associated with Example 4.13 NOCARD

Solution(1)
\(\phi\) x y z
A 17 21 20
B 11 15 14
C 14 18 17
D 12 9 15
Exercise 4-9(2)

Show that a \(\mathcal{V}\) profunctor is the same as a function \(Ob(\mathcal{X})\times Ob(\mathcal{Y}) \xrightarrow{\phi} V\) such that, \(\forall x,x' \in \mathcal{X}, y,y' \in \mathcal{Y}\), the following holds in \(\mathcal{V}\):

\(\mathcal{X}(x',x)\otimes \phi(x,y) \otimes \mathcal{Y}(y,y') \leq \phi(x',y')\)

Solution(1)

  • A \(\mathcal{V}\) profunctor must be a function satisfying the following constraint, according to the \(\mathcal{V}\) functor definition:

    • \(Z((x,y),(x',y')) \leq\) \(\mathcal{V}(\phi((x,y)),\phi((x',y')))\)

    • where \(Z = \mathcal{X}^{op}\times \mathcal{Y}\)

  • Unpacking the definition of a product \(\mathcal{V}\) category, we obtain

    \(\mathcal{X}^{op}(x,x') \otimes \mathcal{Y}(y,y') \leq \mathcal{V}(\phi((x,y)),\phi((x',y')))\)

  • And applying opposite category definition: \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y') \leq \mathcal{V}(\phi((x,y)),\phi((x',y')))\)

  • Noting the definition of \(\multimap\) for a \(\mathcal{V}\) category enriched in itself:

    \(\mathcal{V}(v,w)=v\multimap w\), so now we have: \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y') \leq \phi((x,y)) \multimap \phi((x',y'))\)

  • From the constraint of a hom-element of a symmetric monoidal preorder \(\mathcal{V}\), i.e. \(a \leq (v \multimap w)\) iff \((a \otimes v) \leq w\), we see that the first case pattern matches with:

    • \(a \mapsto\) \(\mathcal{X}(x',x) \otimes \mathcal{Y}(y,y')\)

    • \(v \mapsto\) \(\phi((x,y))\)

    • \(w \mapsto\) \(\phi((x',y'))\)

  • So using the iff we can rewrite as \((a \otimes v) \leq w\), and use the commutativity of \(\otimes\) to obtain the desired expression.

Linked by

Back to co-design diagrams(4)

Each box in a codesign problem has a list of preorders on the LHS and another list on the right.

The box represents a feasibility relation: \(Load \times Velocity \nrightarrow Torque \times Speed \times \$\)

Movie constraints(1)

  • Consider the feasibility relation

    • \(T:=\boxed{mean\rightarrow nice}\)

    • \(E:=\boxed{boring\rightarrow funny}\)

    • \(Money:=\boxed{100 K\rightarrow 500 K \rightarrow 1M}\)

  • A possible feasibility relation is here:

  • This says, e.g., a nice but boring movie costs $500,000 to produce.

  • We can infer that we can also make a mean/boring movie with what we can produce nice/boring movie.

Linked by

Exercise 4-18(2)

The node \((nice,funny)\) has no arrow from it in Example 4.18a. What does this mean?

Solution(1)

It is not feasible, for any amount of money listed, to produce a nice and funny movie.